我們通常需要快速地估計出印刷電路板上一根走線或一個平面的電阻值，而不是進行冗繁的計算。

雖然現在已有可用的印刷電路板布局與信號完整性計算程序，可以精確地計算出走線的電阻，但在設計過程中，我們有時候還是希望采取快速粗略的估計方式。

有一種能輕而易舉地完成這一任務的方法，叫做“方塊統計”。采用這種方法，幾秒鐘就可精確估計出任何幾何形狀走線的電阻值(精度約為10%)。

一旦掌握了這種方法，就可將需要估算的印刷電路板面積劃分為幾個方塊，統計所有方塊的數量后，就可估算出整個走線或平面的電阻值。

塊統計的關鍵概念是：任何尺寸的正方形印刷電路板走線(厚度確定)的電阻值都與其它尺寸的方塊相同。

正方塊的電阻值只取決于導電材料的電阻率及其厚度。這一概念可適用于任何類型的導電材料。

表1給出了一些常見的半導體材料以及它們的體電阻率。

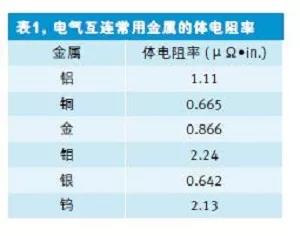
對印刷電路板而言，最重要的材料就是銅，它是大多數電路板的制造原料(注意：鋁用于集成電路片芯的金屬化，本文原理同樣適用于鋁)。

我們先從圖1中的銅方塊說起。該銅塊的長度為L，寬度也為L(因為是正方形)，厚度為t，電流通過的銅箔區截面積為A。

該銅塊的電阻可簡單表示為R=ρL/A，其中，ρ是銅的電阻率(這是材料的固有特性，在25℃時為0.67μΩ/in.)。

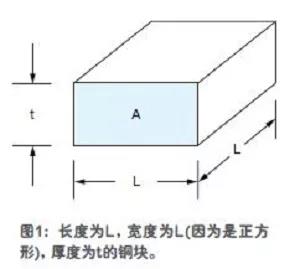
但注意，截面A是長度L與厚度t的乘積(A=Lt)。分母中的L與分子中的L相互消去，只留下R=ρ/t。

因此，銅塊的電阻與方塊的尺寸無關，它只取決于材料的電阻率與厚度。

如果我們知道任何尺寸銅方塊的電阻值，并可將需要估算的整條走線分解成多個方塊，就可加算(統計)方塊數量，從而得出走線的總電阻。

實現

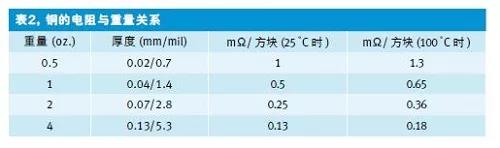
要實現這一技術，我們只需要一個表，表中給出了印刷電路板走線上一個方塊的電阻值與銅箔厚度之間的函數關系。銅箔厚度一般用銅箔重量來指定。例如，1oz.銅指的是每平方英尺重量為1oz.。

表2給出了四種最常用銅箔的重量以及它們在25℃和100℃時的電阻率。請注意，由于材料具有正溫度系數，銅電阻值會隨溫度的升高而增加。

打個比方，我們現在知道一塊0.5oz.重的方形銅箔的電阻大約為1mΩ，這個值與方塊的尺寸無關。

如果我們能把需要測算的印刷電路板走線分解為多個虛擬的方塊，然后把這些方塊加總起來，就得到了走線的電阻。

這樣，總共就有12個方塊。按照表2，每個0.5oz.重的銅箔方塊的電阻為1mΩ，現在共有12個方塊，因此走線的總電阻為12mΩ。

拐彎怎么算?

為便于理解，前文列舉了一個非常簡單的例子，下面我們來看看復雜點的情況。

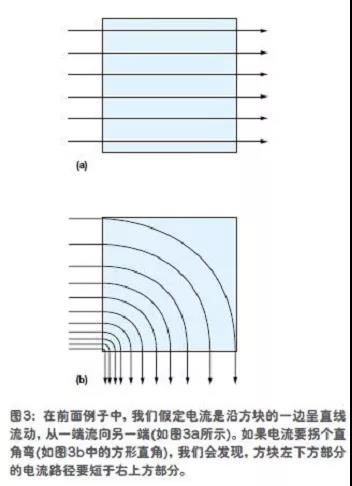
首先要知道，在前面的例子中，我們假定電流是沿方塊的一邊呈直線流動，從一端流向另一端(如圖3a所示)。

然而，如果電流要拐個直角彎(如圖3b中的方形直角)，那情況就有些不同了。

在前面的例子中，我們假定電流是沿方塊的一邊呈直線流動，從一端流向另一端(如圖3a所示)。

如果電流要拐個直角彎(如圖3b中的方形直角)，我們會發現，方塊左下方部分的電流路徑要短于右上方部分。

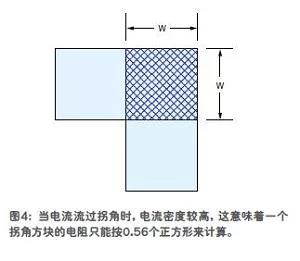
當電流流過拐角時，電流密度較高，這意味著一個拐角方塊的電阻只能按0.56個正方形來計算。

現在我們看到，方塊左下方部分的電流路徑要短于右上方部分。因此，電流會擁擠在電阻較低的左下方區域。

所以，這個區域的電流密度就會高于右上方區域。箭頭之間的距離表示了電流密度的差異。結果是，一個拐角方塊的電阻只相當于0.56個正方形(圖4)。

同樣，我們可對焊在印刷電路板上的連接器做一些修正。在這里，我們假設，與銅箔電阻相比，連接器電阻可忽略不計。

我們可以看到，如果連接器占據了待評估銅箔區域中很大一部分，則該區域的電阻就應相應降低。

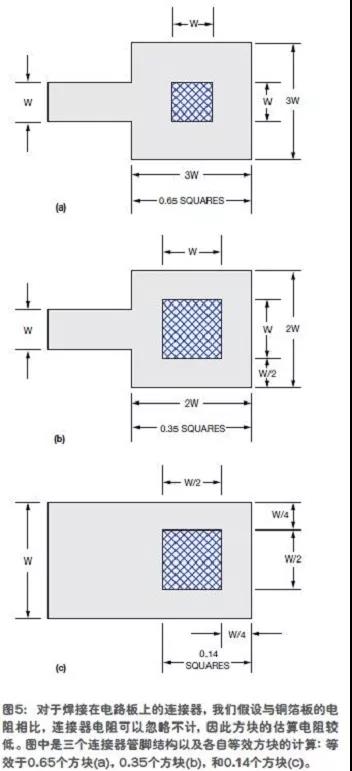
圖5顯示了三端連接器結構及其等效方塊的計算(參考文獻1)。陰影區表示銅箔區內的連接器管腳。

在，我們用一個較為復雜的例子來說明如何使用這種技術。圖6a為一個較復雜的形狀，計算它的電阻需要費點工夫。

這個例子里，我們假設條件是25℃下銅箔重量為1oz.，電流方向是沿走線的整個長度，從A點到B點。A端和B端都放有連接器。

采用前述的相同技術，我們可把復雜形狀分解為一系列方塊，如圖6b所示。這些方塊可以是任何適宜的尺寸，可用不同尺寸的方塊來填充整個感興趣的區域。

只要我們有一個正方塊，并知道銅走線的重量，就能知道電阻值。

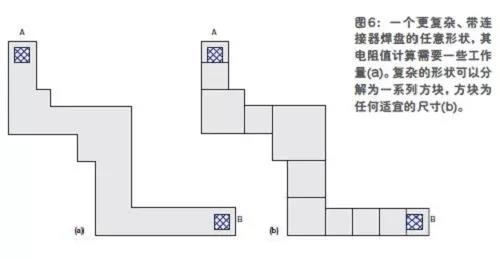
我們共有六個完全正方塊，兩個包括連接器的正方塊，還有三個拐角方塊。

由于1oz.銅箔的電阻為0.5mΩ/方塊，并且電流線性地流過六個全方塊，這些方塊的總電阻為：6×0.5mΩ=3mΩ。

然后，我們要加上兩個有連接器的方塊，每個按0.14個方塊計算(圖5c)。

因此，兩個連接器算0.28個方塊(2×0.14)。對于1oz.銅箔，這增加了0.14mΩ的電阻(0.28×0.5mΩ=0.14mΩ)。

最后，加上三個拐角方塊。每個按0.56個方塊計算，總共為3×0.56×0.5mΩ=0.84mΩ。

因此，從A到B的總電阻為3.98mΩ(3mΩ+0.14mΩ+0.84mΩ)。

●六個為1的全正方形=6個等效方塊;兩個為0.14的連接器方塊=0.28個等效方塊;三個為0.56的角方塊=1.68個等效方塊

●總等效方塊數=7.96個等效方塊

●電阻(A到B)=7.96個方塊的電阻，因每方塊為0.5mΩ，于是總電阻=3.98mΩ

這一技術可以方便地應用至復雜的幾何形狀。一旦知道了某根走線的電阻值，想算其它量(如電壓降或功耗等)就很簡單了。

印刷電路板通常都不限于單層，而是以不同層的方式堆疊起來。過孔用于不同層之間的走線連接。

每個過孔的電阻有限，在走線總電阻計算時必須將過孔的電阻考慮在內。

一般而言，當過孔連接兩根走線(或平面)時，它就構成了一個串聯電阻元件。經常采用多個并聯過孔的方法，以降低有效電阻。

過孔電阻的計算基于圖7所示的簡化過孔幾何形狀。沿著過孔長度(L)方向的電流(如箭頭所指)穿過一個截面積區域(A)。厚度(t)取決于過孔內壁電鍍的銅層厚度。

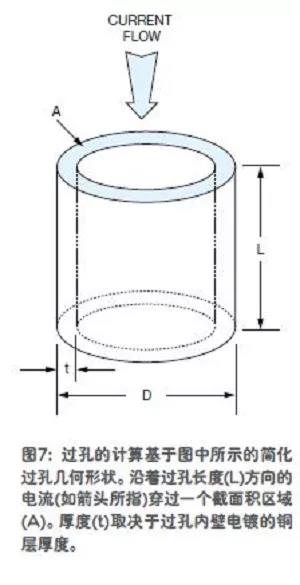
經過一些簡單的代數變換，過孔電阻可表示為R=ρL/[π(Dt-t2)]，其中，ρ是鍍銅的電阻率(25℃下為2.36μΩ/in.)。

注意，鍍銅的電阻率遠高于純銅的電阻率。我們假設，過孔中鍍層的厚度t一般為1mil，它與電路板的銅箔重量無關。對于一個10層板，層厚為3.5mil，銅重量為2oz.時，L大約為63mil。

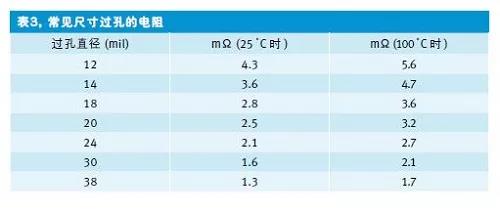
基于上述假設，表3給出了常見過孔尺寸及其電阻。我們可以針對自身特殊的板厚，調整這些數值的高低。另外，網上也有許多免費易用的過孔計算程序。

以上就是一種估算印刷電路板走線或平面直流電阻的簡單方法。復雜的幾何形狀可以分解成多個不同尺寸的銅方塊，以近似于整個銅箔區。

一旦確定了銅箔的重量，則任何尺寸方塊的電阻值就都是已知量了。這樣，估算過程就簡化為單純的銅方塊數量統計。