本文深入介紹了高頻線路板傳輸線的損耗。我們將討論導體損耗、信號走線電阻、介電損耗、介電損耗角正切/耗散因數和總插入損耗。在我們之前的PCB傳輸線系列中，我們為您提供了傳輸線的特征阻抗：

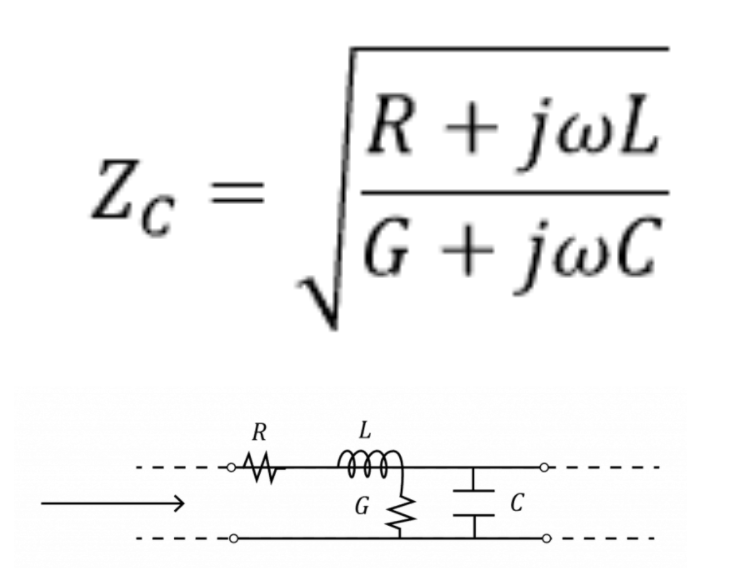
其中：
R = 每單位長度的線路導體電阻 (pul)
L = 線路導體的電感線圈 pul
G = 信號和返回路徑之間的電導（由于介電材料） pul
C = 信號和返回路徑之間的電容 pul（它隨著電介質的 Dk 而增加）

對于均勻傳輸線，R、L、G、C 在其上的每一點都是相同的，因此Zc傳輸線上的每一點都具有相同的值。

對于頻率進行的正弦信號在線的方向上，每個點和時間的電壓和電流表達式都由下式給出：

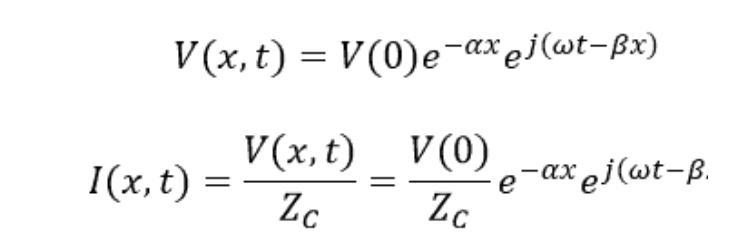
其中 α 和 β 的實部和虛部，由下式給出：

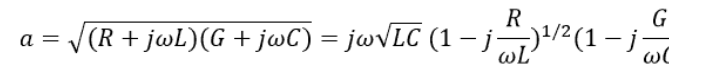
在我們感興趣的頻率上，R <<ωL 和 G <<ωC，所以：

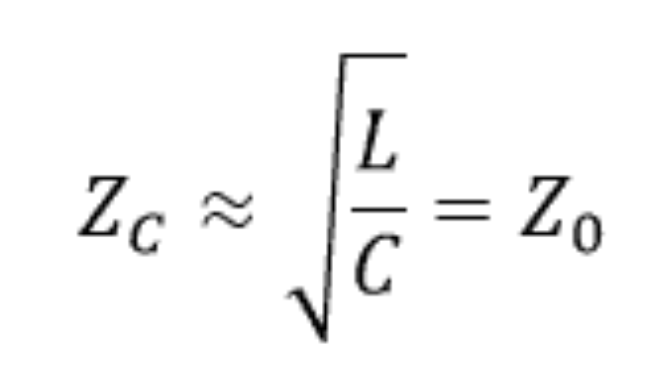
所以：

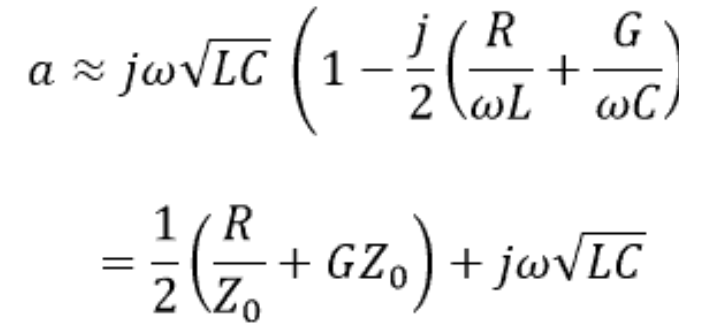
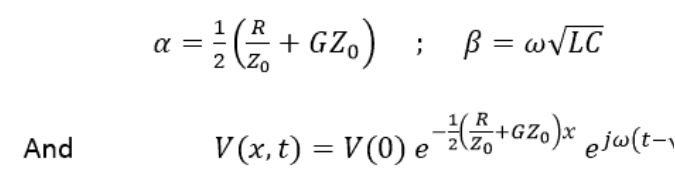
這意味著波長以每單位長度傳播延遲，傳播，并在沿線傳播時衰減。

長度為 l 的傳輸線的信號衰減系數為：

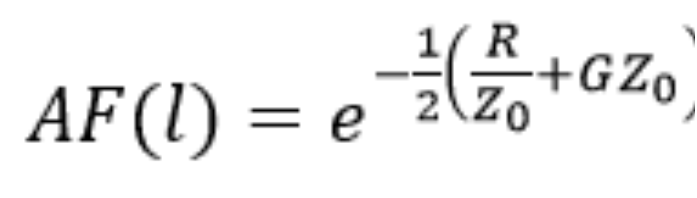
衰減或信號損耗因子通常以 dB 表示。

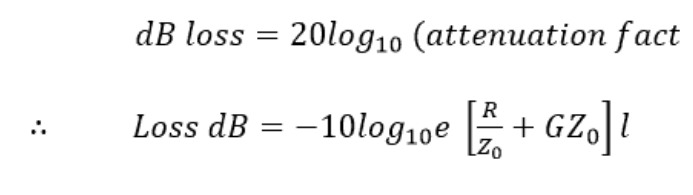
這樣，dB 損耗與線路長度成正比。因此，我們可以將上述單位長度的dB損耗表示為：

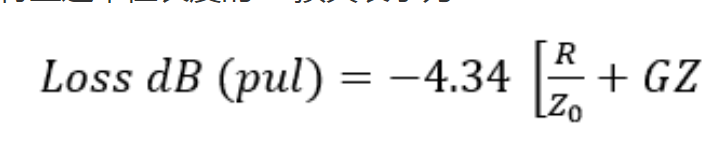
我們通常省略減號，記住它是一個 dB 損失——總是從信號強度中減去 dB。

以上也稱為傳輸線單位長度的總插入損耗，寫為：

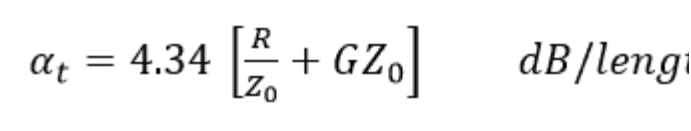
現在 R/Z0 分量的損耗與 R 成正比，單位長度的電阻稱為導體損耗，這是由于構成傳輸線的導體的電阻。它由'alfa'C代表。 GZ0的損耗與G-介電材料的電導成正比，稱為介電損耗-用'alfa'd表示。

導體損耗

其中 R 是每英寸導體的電阻。

現在PCB線路板傳輸線中有兩條線——信號走線和返回路徑。

通常返回路徑是平坦的，但返回電流在平坦表面上分布不均勻——我們可以證明大部分電流集中在三倍寬度的條帶上。

信號走線電阻

信號走線的整個截面積是否平均參與信號電流？答案是：情況并非總是如此——這取決于信號的頻率。

在非常低的頻率下——直到 大約1 MHz，我們可以假設整個導體都參與到信號電流中，因此 Rsigis 與信號走線的'alfa'C 電阻，即：

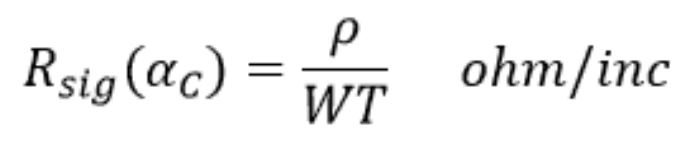
其中：

ρ = 銅電阻，以歐姆-英寸為單位

W = 以英寸為單位的走線寬度（例如：5 密耳，即 0.005 英寸 50 歐姆走線）
T = 以英寸為單位的走線厚度（通常為 ? 盎司至 10 盎司，即 0.0007" 至 0.0014"）

例如，對于 5 密耳寬的走線：

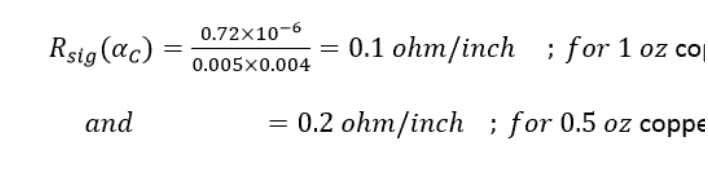
出于我們的目的，我們對頻率 f 下的 A/C 電阻感興趣。在這里，皮膚效果進入了畫面。根據趨膚效應，頻率為 f 的電流只傳播到一定深度，稱為導體趨膚深度，即：

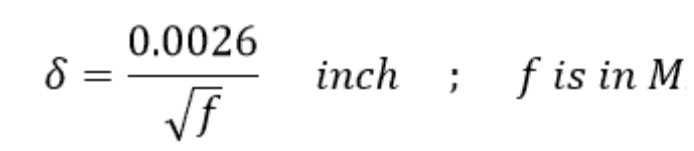
下表顯示了不同頻率下的趨膚深度值：

我們從上面看到，在 4 MH 時，趨膚深度等于 1 盎司銅厚，而在 15 MHz 時，它等于 ? 盎司銅厚。在 15 MHz 以上，信號電流僅在深度小于 0.7 mil 時傳播，并且隨著頻率的增加而繼續減小。

由于我們專注于高頻行為，我們可以安全地假設 T 大于我們感興趣的頻率處的趨膚深度，因此我們將在信號電阻公式中使用趨膚深度而不是 T。

我們使用 2δ 而不是 δ，因為電流使用了導體的所有外圍——技術上 2W 可以用 2 (W + T) 代替。

返回信號僅沿最靠近信號軌道的表面沿厚度 δ 傳播，

由于導體-電介質界面上的銅表面粗糙度導致導體損耗增加，

要知道，在電路板中，“銅導體-電介質界面”從來都不是光滑的（如果是光滑的，銅導體很容易從電介質表面剝離）；它被粗糙化成齒狀結構，以增加電路板上導體的剝離強度。

對于典型的覆銅板，PCB傳輸線損耗如何

其中：

hz = 牙齒的峰值高度

hz 是表面粗糙度的量度。

通常，Hz 從一種箔片類型到另一種箔片類型不同。典型 v價值是：

如果粗糙度 hz 小于趨膚深度（在非常高的頻率下就是這種情況），這將導致額外的導體損耗。我們通過使用不同頻率的不同箔制作測試電路板，通過實驗觀察到這種增加。

我們發現 VLF 箔的損耗低于普通 HTE 箔的損耗。

對于頻率大于 1 GHz 的射頻/微波電路板，這些由于粗糙度導致的導體損耗在長信號線上會變得明顯。

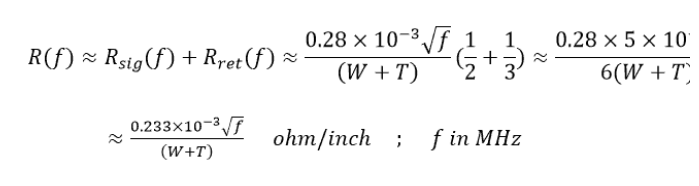
低頻，還是：

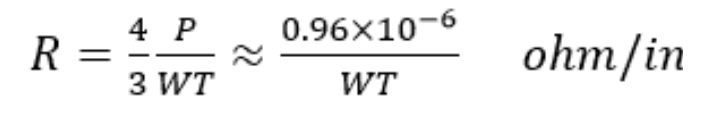
對 R 使用上述等式中較高的一個。

在高頻率下：

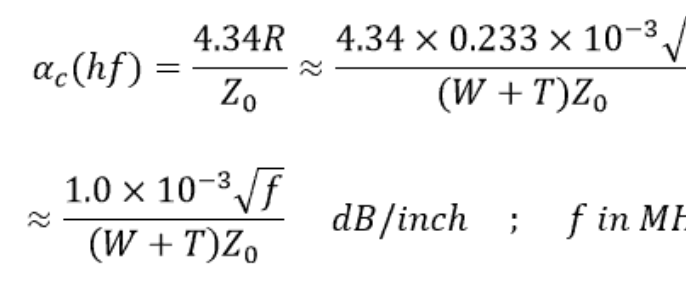
如果 f 是 GHz，W 和 T 是密耳，我們得到：

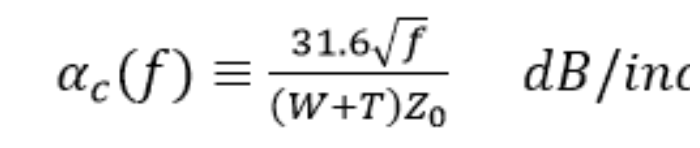
讓我們將其計算為 5 密耳、1 盎司、50 歐姆和 4 密耳、0.5 盎司和 50 歐姆的電線：

需要注意的重要一點是，當頻率大于 50 MHz 時，導體損耗與頻率的平方根成正比：

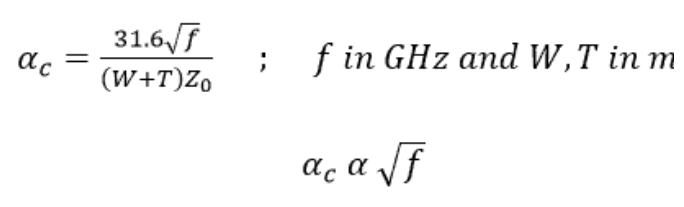
預測由銅粗糙度引起的額外損耗并不容易——沒有簡單的公式。

介電損耗

如前所述，這是傳輸線中每單位長度的介電損耗 dB，

其中：

G = 介電材料的電導率

Z0 = 傳輸線阻抗約為√L/C

PCB介電材料的兩大特點：
1. 介電常數-Dk 或 Er- 也稱為相對介電常數。
2. 損耗因數-Df-也稱為tanδ。

PCB材料制造商公布Er和Df的值。

現在我們將找出 G 和 Er、Df 之間的關系。

介電損耗角正切/耗散因數

我們可以將兩個導體之間的介電層建模為電導 G 和并聯電容 C：

該導體上的交流電壓和頻率電流為：

IG 是通過 G 的電流，IC 是通過電容器的電流。

tanδ 也稱為損耗因數 Df≡tanδ。

如果 σ 是介電材料的有效電導率，

通過實驗觀察，tanδ或Df隨頻率變化很小，可以認為是一個與所有實際目的無關的頻率值：

上式顯示了電導率 σ，因此電介質的電導率 G 隨頻率增加。這是您可以預期的頻率越高，電介質偶極子機械運動中的散熱越大，并且它們與電介質上的交變電場對齊。 （我們稱之為“阻尼振動偶極矩”。）

回想一下√LC 給出了傳輸線單位長度的傳播延遲-Pd -。

我們從上面看到介電損耗與頻率成正比。

為了了解它的尺寸，讓我們考慮PCB材料Isola 370HR和I-Speed和I-Meta：

總插入損耗

導體損耗-'alfa'C-和介電損耗的總和：'alfa'd。

我們衡量損失的價值。 （單獨測量導體和介電損耗并不容易。）

如果我們測量不同頻率下（例如從1 GHz到10 GHz）正弦信號的插入損耗

如果我們現在繪制'alfa'ins/√fvs√f，我們期望得到一個可以確定A1和A2的線性圖。